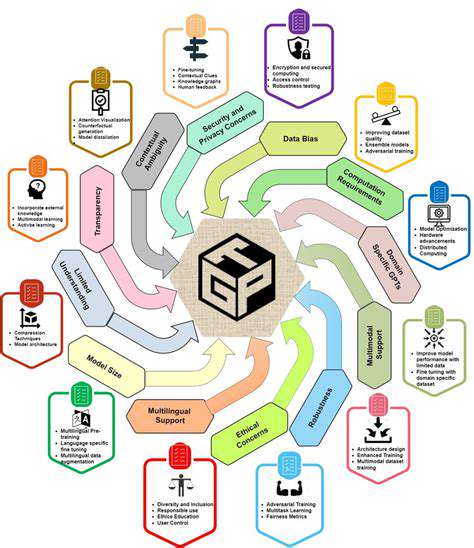
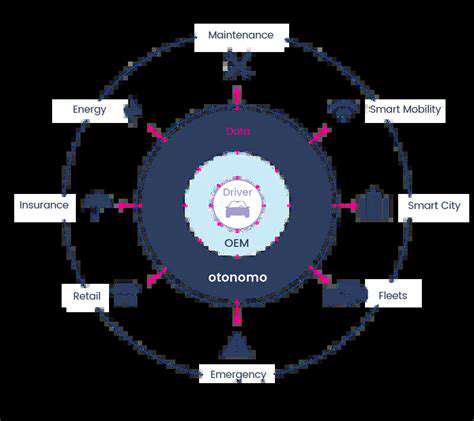
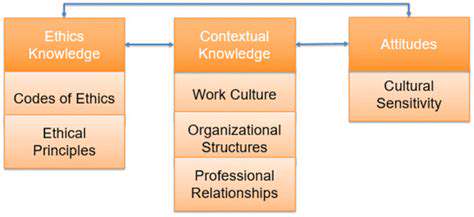
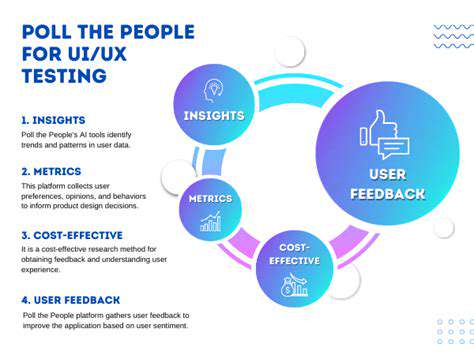
Grid Search
Grid search is a systematic approach to hyperparameter tuning where all possible combinations of hyperparameter values are evaluated. It's a straightforward method, but can be computationally expensive, especially for models with many hyperparameters and a wide range of values to explore. The algorithm exhaustively tests every possible combination of hyperparameters specified in a grid, creating a search space that effectively becomes a grid of potential parameter values. This ensures that no potential optimal configuration is missed, offering a comprehensive evaluation of the hyperparameter landscape. However, its inherent brute-force nature makes it impractical for high-dimensional search spaces or large datasets requiring significant computational resources. This exhaustive search can be time-consuming, particularly when dealing with multiple hyperparameters and a wide range of possible values for each.
A key advantage of grid search is its simplicity. It's easy to implement and understand, making it a popular choice for beginners. The systematic nature of the search also provides clear insights into the performance of different hyperparameter combinations, allowing for detailed analysis of the impact of various settings on the model's performance. However, it's crucial to be aware of the limitations. The computational cost quickly becomes prohibitive as the number of hyperparameters and their possible values increases. In such cases, alternative methods like random search may offer a more efficient approach.
Random Search
Random search, as an alternative to grid search, randomly samples hyperparameter values from a predefined distribution. Instead of evaluating all possible combinations, it focuses on a subset of randomly selected combinations. This approach is significantly faster than grid search, especially for high-dimensional search spaces, as it avoids the exhaustive evaluation of every possible combination. This efficiency stems from its ability to rapidly explore the parameter space, potentially uncovering optimal configurations much quicker than the systematic nature of grid search.
Random search offers an effective compromise between exhaustive exploration and computational efficiency. By randomly sampling hyperparameter values, it can potentially discover optimal configurations without the significant computational burden of grid search. This makes it particularly suitable for large-scale problems where computational time is a critical factor. However, it's important to acknowledge that random search doesn't guarantee finding the absolute best hyperparameter combination. The results are highly dependent on the quality of the random samples and the distribution from which they are drawn.
Comparison and Considerations
Both grid search and random search are valuable hyperparameter tuning techniques, each with its own strengths and weaknesses. Grid search offers a comprehensive evaluation, ensuring that no potential optimal configuration is missed, but it's computationally expensive, especially as the number of hyperparameters and their possible values increase. Random search, on the other hand, is significantly faster, making it suitable for high-dimensional search spaces and large datasets, but it doesn't guarantee finding the absolute best hyperparameter combination.
The choice between grid search and random search often depends on the specific problem and available resources. For smaller-scale problems with a manageable number of hyperparameters and a relatively limited search space, grid search might be a suitable choice. However, for large-scale problems or those with numerous hyperparameters, random search provides a more practical and efficient alternative. Ultimately, the most effective approach depends on factors such as the computational budget, the number of hyperparameters, and the desired level of confidence in finding the optimal configuration.