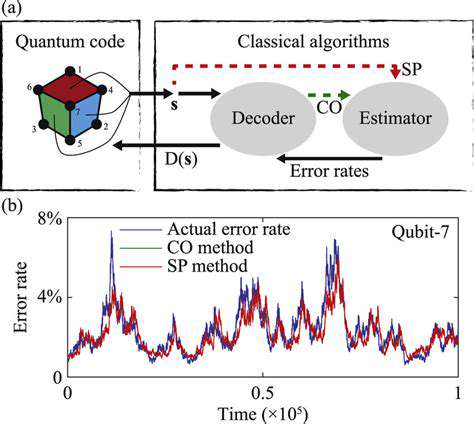
Quantum Error Correction: The Foundation
Building stable and reliable quantum computers hinges on the use of quantum error correction codes. These specialized codes act as a shield, safeguarding quantum information from the destructive impact of errors—an unavoidable consequence of quantum systems' inherent fragility. Environmental interactions frequently introduce these errors, which can rapidly degrade quantum information, leading to inaccurate and ultimately worthless calculations. Without effective error correction, quantum computers would remain impractical for any substantial computational tasks.
At its core, quantum error correction involves encoding quantum information across multiple qubits. This strategic redundancy enables the system to both identify and rectify errors within the encoded data. Through careful encoding techniques, we can construct systems that demonstrate remarkable resistance to noise and other imperfections.
Types of Quantum Error Correction Codes
The field boasts various quantum error correction codes, each offering distinct advantages and limitations. Notable examples include Shor codes, Steane codes, and surface codes, which vary in complexity, error correction potential, and the specific errors they address. Selecting the optimal code for a given quantum computing application demands a thorough understanding of each code's unique characteristics.
The choice often depends on the particular noise profile of the quantum hardware in use. Continuous innovation in this area yields increasingly sophisticated quantum error correction codes tailored to tackle the challenges posed by real-world quantum systems.
Error Detection and Correction Mechanisms
Quantum error correction codes employ ingenious mathematical frameworks to detect and remedy errors. These structures facilitate the identification of compromised qubits and the execution of corrective measures to restore quantum information. These processes frequently rely on redundant information encoding, which forms the basis for effective error detection and correction.
Practical Implementation Challenges
Despite their theoretical elegance, implementing quantum error correction codes presents formidable obstacles. A primary challenge involves the substantial number of qubits required for effective implementation. Sustaining the coherence and stability of numerous qubits over extended durations represents a significant engineering challenge.
Additionally, the computational overhead associated with error correction algorithms can be considerable, potentially impeding overall quantum computation performance. Overcoming these practical difficulties is essential for developing functional, practical quantum computers.
Quantum Error Correction and Quantum Supremacy
Quantum error correction plays a pivotal role in achieving quantum supremacy. By mitigating errors, we enable computations that surpass classical computing capabilities. Attaining quantum supremacy requires a reliable quantum architecture capable of executing complex calculations without constant error interference.
Large-scale error correction capabilities will serve as a critical milestone, signaling quantum computers' superiority over classical systems in specific domains. This achievement would unlock new research possibilities across multiple disciplines.
Future Directions in Quantum Error Correction
Current research focuses on developing more efficient, robust codes and exploring innovative error mitigation strategies. Investigations into topological codes show particular promise, potentially offering enhanced fault tolerance capabilities.
Advances in quantum hardware and control methodologies are equally crucial for practical quantum error correction applications. These ongoing developments hold the key to realizing quantum computing's full potential.
Beyond the Basics: The Challenge of Implementation
Understanding the Theoretical Framework
While conceptually elegant, quantum error correction depends on a solid theoretical foundation. This framework specifies how to encode quantum information to facilitate error detection and correction—essential processes in quantum systems. The encoding typically involves multiple qubits, converting fragile quantum states into more resilient forms that support stable computations.
Core principles, including information redundancy and error detection codes, underpin all practical implementations. Mastering the mathematical foundations and understanding quantum computers' error vulnerabilities are critical for developing effective correction strategies.
Practical Challenges in Qubit Control
The transition from theory to practice presents substantial difficulties, particularly in qubit control. Maintaining qubits' delicate quantum states demands exceptionally stable, isolated environments. External disturbances can introduce errors and decoherence, compromising computation reliability.
Scalability and Resource Requirements
The extensive qubit requirements for practical quantum error correction create significant scaling challenges. As qubit counts grow, so does the complexity of error correction codes and the resources needed to maintain control—an exponential increase that poses a major obstacle to large-scale, fault-tolerant quantum computer development.
Current research explores resource optimization for error correction. Developing efficient, scalable error correction schemes remains crucial for future progress in the field.
Error Correction Code Design and Development
Effective error correction code design is paramount for quantum computation. These codes must balance error detection and correction capabilities with their qubit resource demands. Researchers actively develop diverse code types, each addressing different error scenarios in quantum systems.
Integration with Quantum Hardware
Incorporating error correction protocols into quantum hardware architectures presents complex engineering challenges. Error correction circuits must integrate seamlessly with quantum gate operations, requiring careful consideration of hardware capabilities and limitations. This necessitates close collaboration between error correction theorists and quantum hardware experimentalists.
Developing robust, efficient interfaces between error correction modules and quantum processor architectures is essential for successful implementation.
The Future of Quantum Error Correction
Understanding the Fundamental Problem
Quantum computers offer extraordinary computational potential but remain highly susceptible to errors. Quantum bits (qubits) are particularly vulnerable to environmental interactions that cause decoherence. Unchecked, these errors rapidly lead to computational inaccuracies, rendering quantum computers ineffective. Comprehending these errors and their effects is vital for developing robust quantum architectures.
Decoherence results from qubits' inherent interaction with their environment, causing quantum states to lose coherence and become classical states. This loss of superposition and entanglement—quantum computation's foundational principles—represents a major challenge for practical quantum computing.
Different Approaches to Error Correction
Multiple strategies address these errors. One common approach encodes quantum information across multiple qubits, creating quantum redundancy that enables error detection and correction, similar to classical computing error-correcting codes.
Another strategy involves actively controlling qubit environments to minimize external interactions, requiring sophisticated control systems and specialized setups. Both active and passive error correction methods are essential for reliable quantum computers.
The Role of Quantum Algorithms
Quantum error correction extends beyond qubit protection to influence quantum algorithm design and implementation. Stable qubits are prerequisite for robust quantum algorithms. Algorithms designed without error correction considerations will likely fail on actual quantum computers, necessitating close integration between algorithm design and error correction techniques.
Error-resistant quantum algorithms are crucial for realizing quantum computing's full potential. These algorithms must carefully account for error mitigation. The intersection of quantum algorithm design and error correction techniques represents one of quantum computing's most active research areas.
Challenges and Future Directions
Despite progress, quantum error correction faces significant challenges. Scaling techniques to accommodate large qubit numbers remains problematic—as qubit counts increase, so does error correction protocol complexity, potentially limiting effectiveness.
Developing novel error correction codes capable of handling diverse error sources represents another critical challenge, including addressing unique issues presented by specific quantum hardware platforms. Current research emphasizes efficient, scalable error correction techniques suitable for various quantum architectures.
The Importance of Hardware Development
Quantum error correction success depends on advanced quantum hardware development. Different platforms—superconducting circuits, trapped ions, photonic systems—present distinct challenges and opportunities for implementing error correction schemes.
Developing inherently error-resistant qubits represents a crucial hardware development aspect. Creating robust, scalable control systems for qubit manipulation and measurement in error-prone environments is equally essential. Progress in these areas directly impacts quantum error correction feasibility and efficiency.
Ultimately, quantum hardware advancements are vital for practical quantum error correction implementation and the realization of functional quantum computers.